Binary Search Tree is a simple data structure which is very often used to solve a lot of different problems based on searching and sorting, and also it is a very popular topic for programming coding challenges and interview questions.
Binary Search Tree is a rooted binary tree. It is basically a collection of nodes which are linked to each other. now, you may ask what is a node? Each element of the binary tree is a node that has mainly 3 fields,
Each node in the binary tree has the following properties
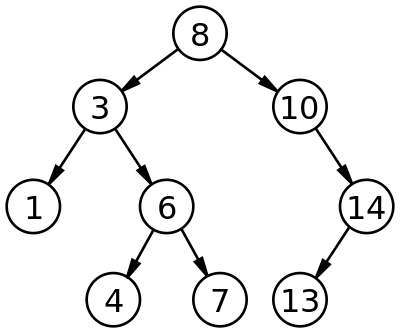
Below is an example image for a binary search tree
In order to traverse and display a binary tree, there are 3 types of traversals which are as follows,
You might also be interested in
Minimum & Maximum Element in BST
Binary Search Tree in Python
Binary Search Tree in C++
Display Leaf Nodes of BST
Height of Binary Search Tree
Linked list in Python
Binary Search Tree is a rooted binary tree. It is basically a collection of nodes which are linked to each other. now, you may ask what is a node? Each element of the binary tree is a node that has mainly 3 fields,
- data or element field
- left link
- right link
Each node in the binary tree has the following properties
- Data of the left node is less than the parent node
- Data of the right node is greater than the parent node.
Below is an example image for a binary search tree
It can be seen in the image above that the data in the left child node is less than the data of the parent node and data of the right child node is greater than the parent node. For example, let us consider 8 as the parent node, then we can see that all the nodes that are to the left of it have a value less than 8 and all the nodes to the right of parent node have a value greater than 8.
There are a lot of advantages of using the binary search tree data structure, they are related to searching, sorting, using them as priority queues, etc.
To know more about binary search tree click here.
This post is an introductory post for Binary search tree so for this post the following operations implemented in the code below.
- Insertion of an element in a Binary search tree.
- Searching for an element in BST.
- Display Binary search tree in Inorder form.
- Display Binary search tree in Postorder form.
- Display Binary search tree in Preorder form.
In order to traverse and display a binary tree, there are 3 types of traversals which are as follows,
- Inorder Traversal: In this type of traversal we print & traverse to the left subtree first, then print the parent node and then print & traverse the right subtree.
- Preorder Traversal: In this type of traversal we print the parent node and then print & traverse the left and right subtree respectively.
- Postorder Traversal: In this type of traversal we print & traverse the left and right subtrees first and then print the parent node.
C++ Program
You might also be interested in
Minimum & Maximum Element in BST
Binary Search Tree in Python
Binary Search Tree in C++
Display Leaf Nodes of BST
Height of Binary Search Tree
Linked list in Python
Comments
Post a Comment