Skip to main content

binary search tree in python

Binary Search Tree is a rooted binary tree. Its subtrees have certain properties. Each element of the binary tree is a node that has mainly 3 fields,

  1. data or element field
  2. left link 
  3. right link
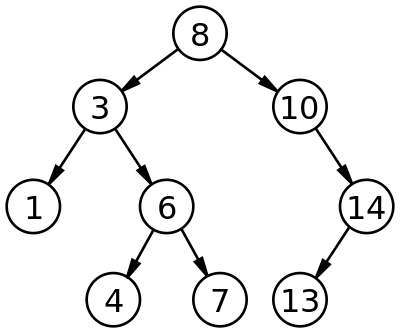
For each node in binary search tree , the data of the left node is less than the parent node and data of the right node is greater than the parent node.




It can be seen in the image above that the data in the left child node is less than the data of the parent node and data of the right child node is greater than the parent node.

There are a lot of advantages of using the binary search tree data structure, they are related to searching , sorting , using them as priority queues , etc.

To know more about binary search tree click here.

The following program has the following operations implemented
  1. isEmpty() : method that checks if the tree is empty.
  2. getRoot() :  method that retuens the root element of the binary search tree.
  3. insert() : Insertion in Binary search tree.
  4. search() : Method for Searching a element in BST.
  5. height() : Method to find the height of the binary search tree.
  6. displayInorder() : Method that displays Binary search tree in Inorder form.
  7. displayPostorder() : Method that displays Binary search tree in Postorder form.
  8. displayProorder() : Method that displays Binary search tree in Preorder form.
  9. displayLeafNodes() : Display the Leaf nodes of the Binary search tree.
  10. maxElement() : method that returns the largest element of the tree.
  11. minElement() : method that returns the smallest element of the tree.
  12. commonAncestor() : method that displays that common ancestor of the two elements.
  13. displayNodesAtDistance() : method that displays nodes at a distance k from the root node.
  14. deleteElement() : method to delete a element from the binary search tree.
  15. deleteMax() : method to delete the largest element of the tree.
  16. deleteMin() :   method to delete the smallest element of the tree.

Python Program

Labels:

Comments

Post a Comment

Popular posts from this blog

Home Page

List of All Programs The Following is the List of all the programs on my Blog Math Programs Square Root of a number using Babylonian Method Finding The Next Smallest Palindrome Finding the Armstrong Numbers Factorial of a number GCD using Euclid's Algorithm Check if a number is Fibonacci Number or not LCM of 2 numbers Trailing Zeros in factorial of a number Sorting Algorithms Bubble Sort Algorithm Selection Sort Algorithm Insertion Sort Algorithm Shell Sort Algorithm Counting Sort Algorithm Linked List Programs Simple Singly Linked List Linked List in C++ Linked List in Python Linked List in Java Doubly Linked List Finding Kth element from the end of Linked List Delete a node from Linked List Delete Kth element from the end of Linked List Rotate Linked List in an Anti-clockwise direction Reversing first K nodes of a Linked List Binary Search Tree Left View of Binary Tree Righ...
4 comments
Read more

Hashing with Quadratic Probing

Hashing is a technique used for storing , searching and removing elements in almost constant time. Hashing is done with help of a hash function that generates index for a given input, then this index can be used to search the elements, store an element, or remove that element from that index. A hash function is a function that is used to map the data elements to their position in the data structure used. For example if we use an array to store the integer elements then the hash function will generate position for each element so that searching, storing and removing operation on the array can be done in constant time that is independent of the number of elements in the array. For better look at the example below. now we face a problem if for 2 numbers same position is generated example consider elements 1 and 14 1 % 13 = 1 14 % 13 = 1 so when we get 1 we store it at the first position, but when we get 14 we see that the position 1 is already taken, this is a case of colli...
Post a Comment
Read more

Hashing with Linear Probing

Hashing is a technique used for storing , searching and removing elements in almost constant time. Hashing is done with help of a hash function that generates index for a given input, then this index can be used to search the elements, store an element, or remove that element from that index. A hash function is a function that is used to map the data elements to their position in the data structure used. For example if we use an array to store the integer elements then the hash function will generate position for each element so that searching, storing and removing operation on the array can be done in constant time that is independent of the number of elements in the array. For better look at the example below. now we face a problem if for 2 numbers same position is generated example consider elements 1 and 14 1 % 13 = 1 14 % 13 = 1 so when we get 1 we store it at the first position, but when we get 14 we see that the position 1 is already taken, this is a case of colli...
Post a Comment
Read more