Minimum and Maximum elements of a Binary Search Tree can be found very easily.
If we see the insertion method of a Binary Search Tree we see that if the new element is greater than the current node data then we move to its right subtree ,Similarly if the new Element is less than the current node data we move to its left subtree.
Hence we can easily infer that the smallest element of the Binary Search Tree must be the leftmost node of the tree.
Similarly we can say also infer that largest element should be the rightmost node of the tree.
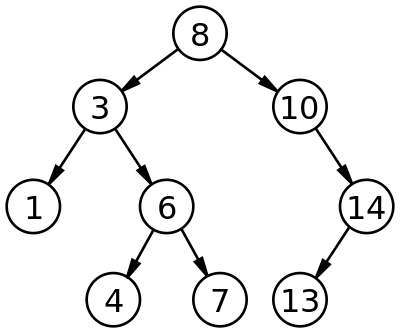
The following image makes the above statement more clear.
In the above figure we see that 1 is the smallest element of the tree which is also the leftmost node of the tree and 14 is the largest element of the tree is rightmost node of the binary tree.
To know more about binary search tree click here.
To see more operations of binary search tree Visit the following Links
Binary Search tree in C++
Binary Search tree in Python
You might also be interested in
Binary Search Tree in Python
Height of Binary Search Tree
Insert ,Search and Display Binary Search Tree
Leaf Nodes of Binary Search Tree
Lowest Common Ancestor in BST
Linked list in Python
If we see the insertion method of a Binary Search Tree we see that if the new element is greater than the current node data then we move to its right subtree ,Similarly if the new Element is less than the current node data we move to its left subtree.
Hence we can easily infer that the smallest element of the Binary Search Tree must be the leftmost node of the tree.
Similarly we can say also infer that largest element should be the rightmost node of the tree.
The following image makes the above statement more clear.
In the above figure we see that 1 is the smallest element of the tree which is also the leftmost node of the tree and 14 is the largest element of the tree is rightmost node of the binary tree.
To know more about binary search tree click here.
To see more operations of binary search tree Visit the following Links
Binary Search tree in C++
Binary Search tree in Python
C++ Program
You might also be interested in
Binary Search Tree in Python
Height of Binary Search Tree
Insert ,Search and Display Binary Search Tree
Leaf Nodes of Binary Search Tree
Lowest Common Ancestor in BST
Linked list in Python
Comments
Post a Comment